Nascido na Roménia de pais gregos, sua família retornou para a Grécia quando tinha dez anos. Lá estudou engenharia em Atenas. Os estudos foram interrompidos pela ocupação nazista. Participou na resistência grega na Segunda Guerra Mundial e na primeira fase da Guerra Civil Grega como membro da companhia de estudantes Lord Byron do Exército de Libertação do Povo Grego. Em Janeiro de 1945 foi ferido por um obus, perdendo um olho e desfigurando-lhe parte do rosto. Em 1946 finalizou os estudos de engenharia, mas foi perseguido e condenado à morte devido ao seu ativismo político, fugindo para França em 1947.
Música Estocástica:
“Estocásticos são padrões que surgem através de eventos aleatórios. Por exemplo, o lançar de dados resulta em numéricos estocásticos, pois qualquer uma das 6 faces do dado tem iguais probabilidades de ficar para cima quando de seu arremesso.
Porém, é importante salientar uma diferença entre aleatoriedade e estocasticidade. Normalmente, os eventos estocásticos são aleatórios. Todavia, podem eventualmente não o ser. É perfeitamente plausível, embora improvável, que uma série de 10 arremessos de dados gere a seqüência não aleatória de 6,5,4,3,2,1,2,3,4,5 ou 1,1,1,1,1,1,1,1,1,1. Apesar de coerente – ou comprenssível (podendo ser expressa de um modo mais comprimido que a seqüência inteira) – a seqüência não-aleatória é estocástica, pois surgiu através de um evento aleatório: o lançar de dados.” [1]
Esse é um exemplo retirado do livro “Formalized Music. Thought and Mathematics in Music” do próprio Xenakis que mostra probabilidades nos arremessos de dados.
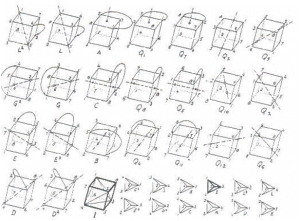
Exemplo Musical 31: Dados Formalize Xenakis, Iannis. “Formalized Music. Though and Mathematics in Music”, Nova Iorque: Pendragon (1992) pag.220
Descrição da peça pelo próprio Xenakis:
“A única fonte para esta composição poliritmica é a idéia de periodicidade, repetição, duplicação, em cópias fiéis, pseudo-fiéis, infiéis…”. A concepção de Xenakis é inusitada, mas “Pleiades” é uma peça maravilhosa que pode ser apreciada mesmo sem a percepção consciente das “nuvens, nebulosas e galáxias de batidas fragmentadas organizadas pelo ritmo”.[2]
Xenakis descreve também sua visão sobre a organização dos eventos musicais com a composição através de recursos probabilísticos, onde o efeito das coincidências matemáticas podem desenvolver periodicidades em meio ao caos. Além das coincidências matemáticas devemos refletir também sobre as probabilidades perceptuais que os ouvintes farão no momento de suas audições. Uma destas coincidências em meio ao caos foi o alvo da analise no experimento com esta peça.
peça é arquitetada em quatro movimentos: Metaux (for metais), Claviers (percussões de teclado), Peaux (tambores) e Melanges (misture).
Utilizei apenas o segundo movimento, Clavier, composto para instrumentos de teclado de metal.
A presente análise mostra recortes da WAV sonora obtida da gravação utilizada nos experimentos, já que neste tipo de execução parte da organização temporal dos eventos depende do interprete no dado instante da execução. Desta forma os efeitos perceptuais serão melhores relacionados com as localizações reais que aqui estarão sendo vistas através da imagem gerada por um WAV.
A primeira seção mostra um único padrão tocado simultaneamente, o que da ao ouvinte uma pulsação inicial constante e de fácil organização.

Figura 33: Primeiro padrão WAV, Pleiades- Imagem criado pelo próprio autor retirada da tela do programa utilizado nos experimentos (Cubase SX)
A onda de cima mostra o inicio dos ataques e a de baixo o som contínuo.
Após estas vinte batidas iniciais uma defasagem dá origem a um novo padrão. A defasagem se origina por uma mudança na velocidade, gerando um primeiro contraste de padrões de 5 contra 4 notas mostradas na figura (34).
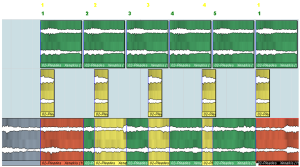
Figura 34: Primeira defasagem, gerando 4 X 5, Pleiades
Esta defasagem se mantém por 3 ciclos e uma nova defasagem cria então uma outra textura polirrítmica. Tais padrões dificilmente serão percebidos separadamente, pois serão executados com um timbre muito parecido.
Neste caso o timbre é um fator determinante na percepção, pois ele junta ou separa notas próximas, definindo padrões na percepção. Um exemplo é uma tercina de colcheias tocada simultaneamente a quatro semicolcheias. O timbre pode variar as audições em dois padrões distintos ou um único mais complexo.
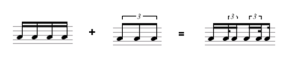
Exemplo Musical 32: Padrões polirritmicos e Timbre
Nesta parte do áudio o som ganha uma característica de “nuvens, nebulosas e galáxias de batidas fragmentadas organizadas pelo ritmo” como ele mesmo descreve. Esta organização ao mesmo tempo em que não define padrões, permite que a interpretação do ouvinte diferencie padrões em meio ao caos como enxergamos figuras e formas nas nuvens quando olhamos para o céu. Uma percepção parecida ocorre numa brincadeira de ligar os pontos, onde só se enxerga a forma depois de ligá-los. Na capa do disco da gravação de “Pleades” utilizada, temos a foto do aglomerado estelar citado. Um aglomerado de estrelas deste tipo pode ser visto através de varias probabilidades de organizações de padrões.
A lei da Gestalt aqui utilizada é a de “experiências passadas” relacionada a uma “configuração de Gestalt na rede”. Uma característica já citada do sistema perceptual humano, no modo de decodificação dos dados assimilados é o fato de relacionarmos os dados recém-assimilados aos de nossa memória para decodifica-los. No entanto o dado novo inserido neste capitulo é a formulação de complexos a partir de suas partes, mesmo se o complexo total não tiver sendo observado. Por exemplo, se já tivermos visto a forma inteira de um elemento, ao visualizarmos somente uma parte dele reproduziremos esta forma inteira na memória.
“Num processo que envolve o pensamento analógico, o trabalho mental não se limita a recuperar um análogo como um todo já preparado para ser utilizado no outro. A memória pode ser chamada para compilar um complexo de informações que não estavam conectados a priori, sendo uma quantidade de informação recuperada não somente de um análogo, mas de vários que se integram para aplicarem-se ao problema em questão e também a outros.”[3]
Ao olhar a capa do disco posso ver um rosto formado por estrelas mesmo que ele não se forme por inteiro e ao mesmo tempo outra pessoa pode enxergar outra forma nas estrelas pela decodificação de sua memória.

Figura 35: Capa do disco PLÉIADES com foto de aglomerado estelar
Um apud de Mecacci demonstra essa característica que interage percepção com intelecção de forma muito interessante referindo-se a transferência de aspectos aparentemente não relacionados, que acabam se conectando constituindo a tal analogia. Gauss, a respeito de um teorema que não conseguia resolver durante anos, escreveu:
“Finalmente, há dois anos, consegui resolvê-lo, por obra dos meus esforços dolorosos e pela graça de Deus. Como uma centelha súbita de iluminação, o enigma resolveu-se. Eu mesmo não sei dizer qual foi o fio condutor que conectou o que eu sabia precedentemente com o que tornou meu êxito possível.”
Gauss apud Mecacci 1987
Mecacci explica tal acontecimento da seguinte forma:
“Colocam-se, diante do pensamento, inúmeros fragmentos aparentemente sem conexão entre si, como eram para Gauss, os elementos de seu Teorema. Depois, vê-se repentinamente a solução, os elementos se ligam entre si, recompõem-se numa unidade, numa estrutura organizada que, precedentemente, era literalmente invisível.”
Mecacci, 1987
[1] Artigo publicado no site http://educincosentidos.blogspot.com/ 16 Outubro 2005 consultado dia 20/10/2008 Autor: Gilberto Câmara
[2] Obtido em “http://pt.wikipedia.org/wiki/Estoc%C3%A1stico” (20/10/2008)
[3] -ABDOUNUR, Oscar João. Matemática e Música
São Paulo: Escrituras, 1999, – pag.158